このサイトではアフィリエイトによる広告を使用しています。
第二種電気工事士の筆記試験対策用に役立てていただけるよう解説していくシリーズ第7弾です。
今回は、交流回路の計算方法 インピーダンス、電力、力率 について解説していきます。
インピーダンスの三角形・力率
交流回路での回路全体の電流の通りにくさをインピーダンスといいます。
下図のように、抵抗とコイルを直列に接続した場合、インピーダンス=Zは、オームの法則より以下となります。
\(\displaystyle インピーダンスZ=\frac{電圧V}{電流I}[Ω]\)
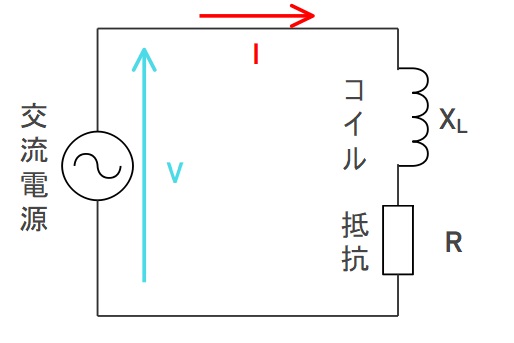
RとXL(コイルのリアクタンス)で直角三角形を表すと斜辺がインピーダンスZとなります。
\(\displaystyle インピーダンスZ=\sqrt {R^2+{X_L}^2}[Ω]\)
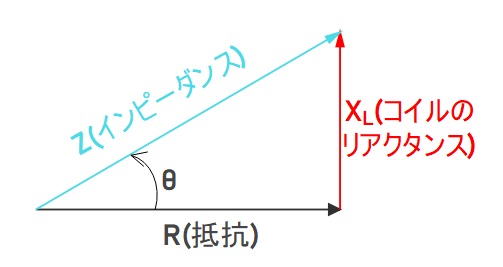
・力率
インピーダンスの三角形の角度θを力率角といい、cosθを力率といいます。
どれだけが有効な電力となるかを表す率で、0~1の値となる。
\(\displaystyle 力率cosθ=\frac{R}{Z}=\frac{R}{\sqrt{R^2+{X_L}^2}}\)
後述する電力の三角形に出てくる力率と同じものです。力率はいくつか式があり、どの式も覚える必要がありますが、三角形のcosθが力率となります。
抵抗とコンデンサを直列接続した回路についても、同様の式が成り立ちます。(今回は略)
※参考
・リアクタンス
コイル、およびコンデンサーの交流電流の通しにくさを表すもので、コイルの場合は誘導性リアクタンス(XL)し、コンデンサーの場合は容量性リアクタンス(XC)といいます。

交流回路の電力
前提として交流回路では、負荷が3種類(抵抗、コンデンサ、コイル)あり、それぞれ性質が異なるため直流の電力の式とは異なります。
交流の電力には、以下の3種類があります。
・皮相電力(見かけの電力)
\(S=VI[V・A]\)
・有効電力(エネルギーとなる電力)
\(P=VIcosθ[W]\)
・無効電力(エネルギーとならない電力)
\(Q=VIsinθ[var]\) (単位:バールと読む)
この式だけ見ると、文系の方はうわっとなるかもしれませんが式は覚えましょう!(鬼、)安心してください!演習問題をひたすらこなせば理解できていきますよ。ここらあたりで、試験では合否に差が出てきます。当サイトは頑張る皆さんを応援します!
電力の三角形、力率、無効率
皮相電力S、有効電力P、無効電力Qについては、以下の 電力の三角形 にて表すことができます。

・力率
皮相電力VIのうち、どれだけが有効な電力となるかを表す率で、0~1の値となる。
力率cosθのθは力率角といいます。
P(有効電力(底辺)) ÷ S(皮相電力(斜辺)) =力率 となります。
\(\displaystyle 力率cosθ=\frac{P(有効電力)}{S(皮相電力)}\)
・無効率
Q(無効電力)とS(皮相電力)の比を無効率という。
\(\displaystyle 無効率sinθ=\frac{Q(無効電力)}{S(皮相電力)}\)
・式の覚え方(参考)
以下のように力率cosθの場合は、S(皮相電力)からP(有効電力)に向かってcosθのcを描くようにSぶんのPとなります。(現役高校生のが詳しいかも、、)
無効率sinθの場合、S(皮相電力)からQ(無効電力)に向かってsinθのs(筆記体)を描くようにSぶんのQとなります。


例題1
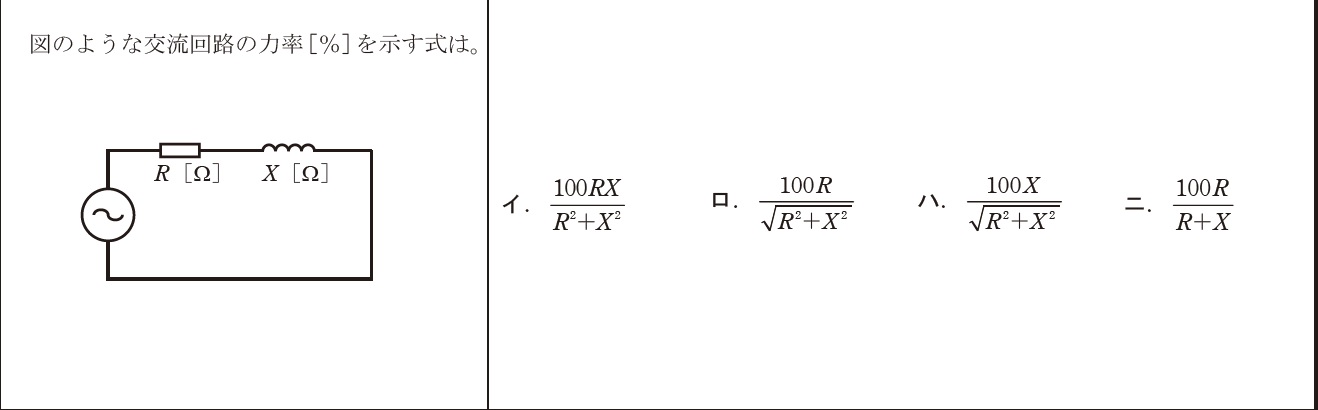
まずはインピーダンスを求めます。
インピーダンスの三角形より
\(\displaystyle インピーダンスZ=\sqrt {R^2+X^2}[Ω]\)
力率は、インピーダンスの三角形より
\(\displaystyle 力率cosθ=\frac{R}{Z}=\frac{R}{\sqrt{R^2+X^2}}\)
力率を[%]表示する場合は100倍します。
\(\displaystyle 力率cosθ=\frac{100R}{\sqrt{R^2+X^2}}\)
交流回路の問題はまずは インピーダンスの三角形、力率を求められるようにしておきましょう。
例題2

\(電圧V=200[V]\)
\(消費電力P=有効電力P=2\times 10^3[W]\)
\(\displaystyle 力率cosθ=\frac{80}{100}=0.8\)
交流回路の電力の式より
\(P=VIcosθ[W]\)
求めたいのは電流I[A]なので、I=の式にすると
\(\displaystyle I=\frac{P}{Vcosθ}=\frac{2\times 10^3}{200\times 0.8}=\frac{10}{0.8}=12.5[A]\)
ポイントは、まず単相200Vということなので交流回路となります。
消費電力=有効電力 です。
力率が%表示されている場合、100で割ることで力率(0~1)を算出します。
例題3

まずはインピーダンスの三角形よりインピーダンスを求めます。
\(\displaystyle インピーダンスZ=\sqrt {8^2+6^2}=\sqrt {64+36}=\sqrt {100}=10[Ω]\)
電圧100[V],インピーダンス10[Ω]より、回路に流れる電流Iはオームの法則より
\(\displaystyle 電流I=\frac{電圧}{インピーダンス}=\frac{100}{10}=10[A]\)
抵抗8[Ω](抵抗のみ、リアクタンス(6[Ω])ではない),電流10[A]より、消費電力Pは
\(消費電力P=I^2R=10^2 \times 8=800[W]\)
ポイントは、インピーダンスを計算、つづいて電流値を計算、最後に消費電力を計算という流れをまずは覚えることです。最後の消費電力の計算には電圧ではなく、抵抗の値(8[Ω]の方)を使用します(抵抗が消費する電力=回路の消費電力)。
例題1,3,4はどれかが問題として出る確率が非常に高いです。繰り返し問題を解いてかならず解けるようにしておきましょう。
例題4
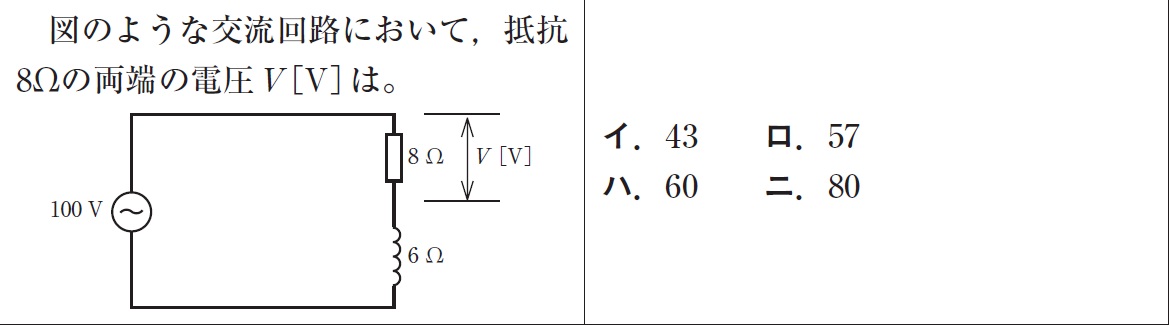
まずはインピーダンスの三角形よりインピーダンスを求めます。
\(\displaystyle インピーダンスZ=\sqrt {8^2+6^2}=\sqrt {64+36}=\sqrt {100}=10[Ω]\)
電圧100[V],インピーダンス10[Ω]より、回路に流れる電流Iはオームの法則より
\(\displaystyle 電流I=\frac{電圧}{インピーダンス}=\frac{100}{10}=10[A]\)
抵抗にかかる電圧Vはオームの法則より
\(V=IR=10 \times 8=80[V]\)
ポイントは、例題1,3と同様です。
全体のポイント
交流回路の問題はかならず出題されます。複雑で理解するのは大変かと思いますが電気工事士の筆記試験においては避けては通れない箇所で、3相交流回路を含めてここを理解できているかどうかで合否に関わってきますし、何より電気工事士の知識として非常に大事です。
時間をかけてじっくり確実に理解していってください。

コメント