当ブログではアフィリエイトによる広告を使用しています。
第二種電気工事士の筆記試験対策用に役立てていただけるよう解説していくシリーズ第6弾です。
今回は、電力(消費電力、有効電力)、ジュールの法則 について解説していきます。
電力、消費電力、有効電力、電力量
・電力、消費電力、有効電力
1秒間に消費する電気エネルギーを電力、消費電力、有効電力といい、単位は[W](ワット)。
(以下より、電力、消費電力、有効電力の呼び方を電力に統一)
電力をP[W]、電圧をV[V]、電流をI[A]とすると以下の式で表されます。
\(電力P=VI[W]\)
\(電力P=I^2 R[W]\)
\(\displaystyle 電力P=\frac{V^2}{R}[W]\)
上記3つの式はどれも同じ意味です。オームの法則 \(V=IR\)より式を展開することができます。これらの3式はよく出てきますので覚える もしくは式を展開できるようにしておきましょう。
・展開方法1
\(電力P=(V)I=(IR)I=I^2 R\)
・展開方法2
\(\displaystyle 電力P=V(I)=V(\frac{V}{R})=\frac{V^2}{R}\)
・注意事項
これらは直流回路、および交流回路の抵抗が消費する電力に適用されます。交流回路の電力については当てはまらないので注意が必要です。
・電力量
電力に時間t[s]をかけると電力量Wになります。
\(\displaystyle 電力量W=VIt=I^2 Rt=\frac{V^2}{R}t[W・s]\)
単位は[W・s](ワット秒)、または[J](ジュール)となります。
実用的な単位としては[W・h](ワットアワー)、[kW・h](キロワットアワー)が使われます。
t[s](秒),T[h](時間)とすると
\(W[W・s]=x[W]\times t[s]\)
\(W[W・h]=x[W]\times T[h]\)
\(W[kW・h]=x[kW]\times T[h]\)
となります。実際の問題では単位がバラバラだったりするので問題を解いて慣れていくのが良いかと思います。

ジュールの法則
・ジュールの法則
抵抗R[Ω]に電流I[A]がt[s]流れる時、発生する熱エネルギーH[J]は
\(H=I^2 Rt[J]\)
となります。お気づきの方もいると思いますが、先に出てきた電力量の式と同じとなります。
熱量計算
・電熱器による発熱量
\(P[kW] \times t[s] \times η\) (電力 x 時間 x 効率)
η(イータ)=熱効率のことで単位は%
・(水などの)温度上昇に要する熱量
\(m[kg] \times c[kJ/(kg・K)] \times θ[K]\) (質量 x 比熱 x 温度上昇)
cは比熱を表す記号(スモールシー)で、比熱とはある物質1gの温度を1℃上昇させるのに必要な熱量のこと([kg・K]だと1kgの物質の温度を1K上昇させるのに必要な熱量)。試験では、水の比熱(4.2[kJ]がよく出るが、値は覚える必要はない。
単位[K]とはケルビンと読み、絶対零度(-273.15[℃])を 0[K] として定義している。
[℃]と[K]の温度上昇、下降の幅は同じ(例えば 10[℃]上昇、10[K]上昇は同じ意味)となる。問題が出た時に [K] って何?とならないようになんとなく覚えてください。
上記2つの式には以下の関係があります。
電熱器による発熱量=温度上昇に要する熱量
\(Ptη=mcθ\)
式をそのまま覚えるのは難しいかと思いますので、過去問を解いて慣れていくのがよいかと思います。例題4に記載していますので参考にしてください。
例題1

まずは時間[h]を秒[s]に変換します。
1時間20分=80分=(80 x 60)秒=4800[s]
ジュールの法則より、
\(H=I^2 Rt=VIt=100 \times 4 \times 4800 =1920000[J] = 1920[kJ]\)
ポイントは時間を秒に変換すること、ジュールの法則=電力量 の式を自在に変換することに慣れていくことですね。
例題2

こちらもまずは時間[h]を秒[s]に変換します。
1時間30分=90分=(90 x 60)秒=5400[s]
ジュールの法則より、
\(H=I^2 Rt=消費電力(電力または有効電力) \times t=500 \times 5400=2700000[J]=2700[kJ]\)
こちらも例題1同様、時間を秒に変換、ジュールの法則を自在に変換できるようにしておきましょう。
例題3
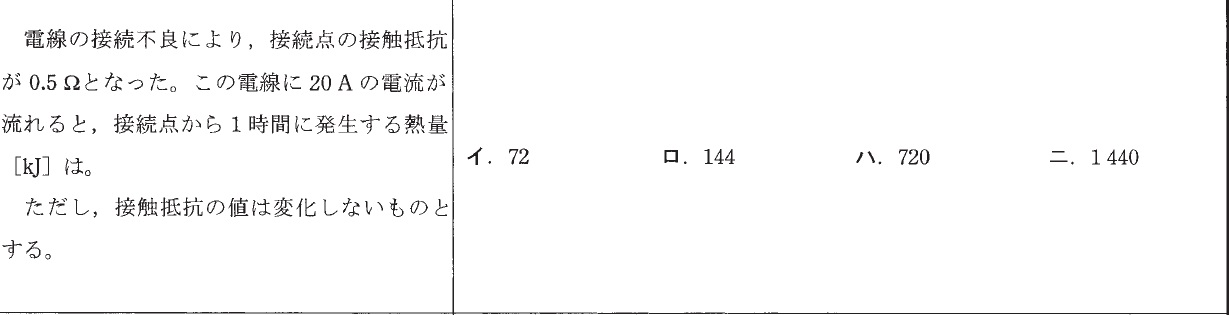
時間[h]を秒[s]に変換します。
1時間=60分=(60 x 60)秒)3600[s]
ジュールの法則より、
\(H=I^2 Rt=20^2 \times 0.5 \times 3600=720000[J]=720[kJ]\)
例題4

まず電力量[kW・h]とありますが、hは1時間の単位を示しますので、こちらを秒の単位に変換します。
\(時間=t[h]=60 \times 60 \times t = 3600t[s]\) となります。
時間の単位が[h]の時は秒[s]に変換すると覚えておいてください。(電熱器による発熱量の式 t の単位は秒[s]のため)
\(η=熱効率100\%=1\) となります。
電熱器による発熱量の式に当てはめると
\(P \times t \times η=P \times 3600t \times 1\)
温度上昇に要する熱量の式に当てはめると
\(m \times c \times θ=60 \times 4.2 \times 20\)
電熱器による発熱量の式=温度上昇に要する熱量の式 より
\(P \times 3600t \times 1 = 60 \times 4.2 \times 20\)
\(\displaystyle Pt=\frac{60 \times 4.2 \times 20}{3600}=\frac{4.2}{3}=1.4[kW・h]\)
ポイントは、時間の単位[h]を[s]に変換すること、式を覚えておくことでしょうか。
この問題はかなり曲者ですが、慣れましょう、、。
全体まとめサイトのご紹介


コメント