このサイトではアフィリエイトによる広告を使用しています。
第二種電気工事士の筆記試験対策用に役立てていただけるよう解説していくシリーズ第2弾です。
今回は合成抵抗の問題を解いていきましょう。
問題1
いきなりですが、以下の問題を解いていきましょう。
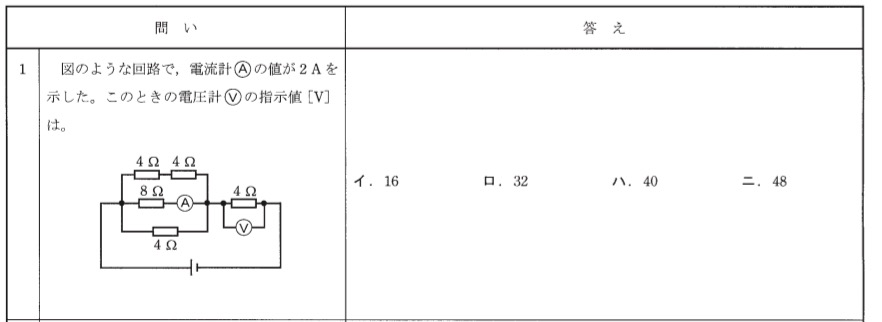
合成抵抗とオームの法則を合わせたような問題ですね、、。
抵抗値が全て出ているので全部の合成抵抗を求めたくなりますが、、落ち着きましょう。
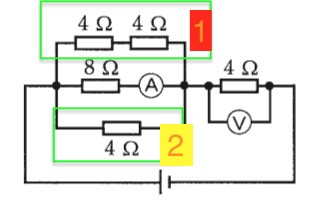
まずは1の部分に注目すると 直列接続となっているので合成抵抗は以下となります。
4+4=8[Ω]
この抵抗値は直ぐ下の抵抗値8[Ω]と同じとなっています。抵抗値が同じため
この1の部分に流れる電流も直ぐ下の抵抗値に流れる電流と同じとなり、2[A]
となります。
続いて2の部分に注目すると、こちらは抵抗値が4[Ω]となっています。
この値は上2つの抵抗値の半分となっているので、ここに流れる電流は
2倍の4[A]となります。
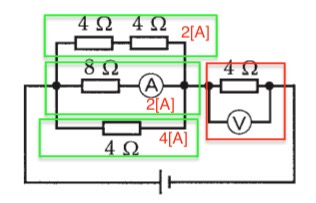
緑で囲った箇所の電流値を全て足すと
2+2+4=8[A]
となります。この合計値が赤枠で囲った箇所の電流値となります。
赤枠で囲った箇所の電圧Vは次のようになります。
V=IR より V=8[A]x4[Ω]=32[V]
よって、Vの電圧は 32[V] となります。
問題2
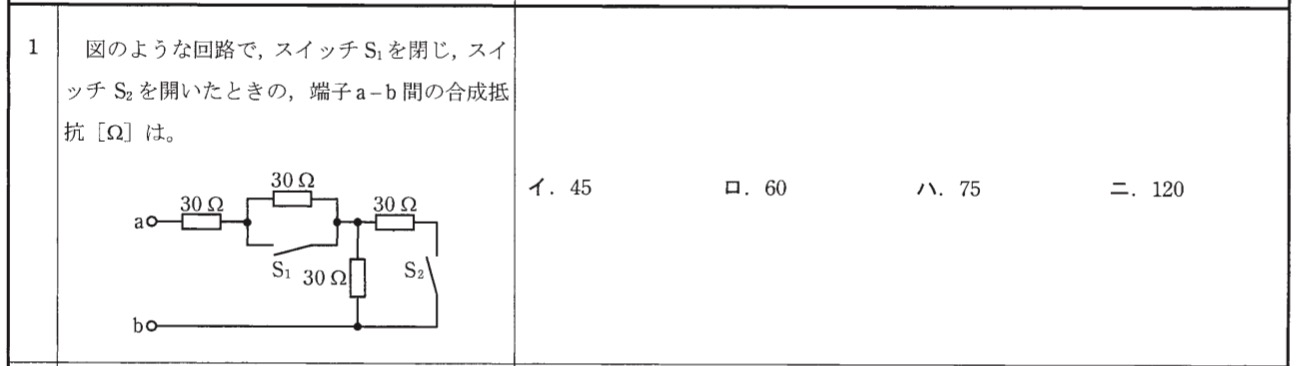
パッと見、難しそうな回路に見えますね。この場合はまず見慣れている回路図に
すると分かりやすくなるかと思います。← それってアナタの感想ですよね、、。
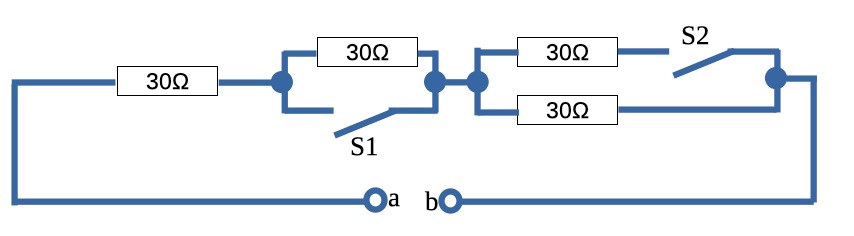
慣れていない方は上記のように書き直すと理解しやすいと思います。
ここからさらに、スイッチS1を閉じ、スイッチS2を開いた場合ですが、
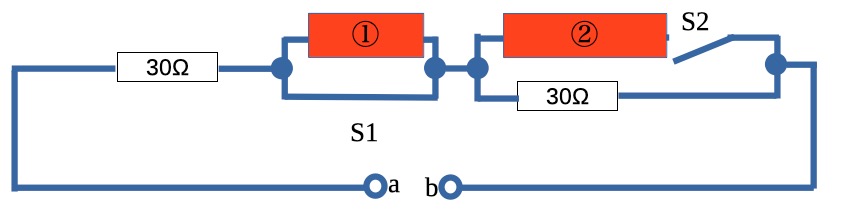
こんな感じ、、、。ちょっと見にくいか、、。
①とS1が並列接続となっています。S1には抵抗がありません。この場合、①の箇所に
どんな抵抗がある場合でも、電流はS1側にしか流れません。よってこの並列接続は
何も接続がされていないものと見なすことが出来ます。
②の箇所ですが、直ぐ後ろの “S2が開いている=回路が繋がっていない” ため
ここの箇所には何も無いと見なすことが出来ます。
上記を踏まえ、回路図をさらに見やすくすると
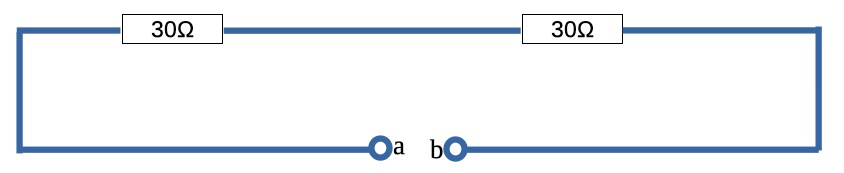
ここまで来ればもうお分かりかと思います。
答えは 30 + 30 = 60[Ω] となります。
①、②の箇所の考え方は結構大事で、後々出てくるスイッチなんかにも出てきますので
覚えておきましょう。
①の場合、厳密には①側にも電流は流れるのですが、今回の電気工事士試験の上では
①には電流は流れないと判断して問題ありません。興味のある方は調べてみると
より理解が深まるかと思います。

コメント