当ブログではアフィリエイトによる広告を使用しています。
第二種電気工事士の筆記試験対策用に役立てていただけるよう解説していくシリーズ第5弾です。
今回は電線の電気抵抗について理解していきましょう。
電線の抵抗
電線の抵抗は以下の式で表されます。
\(\displaystyle 抵抗R =抵抗率ρ\frac{長さℓ}{断面積S}[Ω]\)
式から読み解くと、電線の抵抗R[Ω]は、長さ、断面積と以下の関係があります。
・長さℓ[m]が長くなるほど抵抗R[Ω]が増加(比例)
・断面積S[m\(^2\)]が大きくなるほど抵抗[Ω]が減少(反比例)
式を暗記するよりも長さと断面積の関係のほうがイメージしやすいかと思います。
抵抗率ρ(ローと呼びます)は、電流の通しにくさを表す定数で抵抗率といい、単位は[Ω・m]、抵抗率が高いほど抵抗R[Ω]が増加します。
以下に電線のイメージ図を示します。
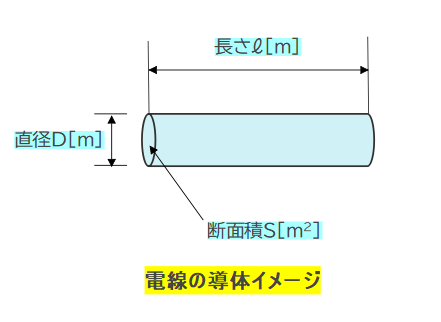
電線の導体の断面積S[m\(^2\)]は、S\(=円周率 \pi \times 半径^2\) より
S\(=\pi \times \displaystyle (\frac{D}{2})^2 = \frac{\pi D^2}{4}\)[m\(^2\)]
応用として断面積の計算方法も覚えておきましょう。
電線の抵抗値比較
電線の抵抗は、電線が長くなるほど抵抗が大きく、電線が太くなるほど抵抗が小さくなる。
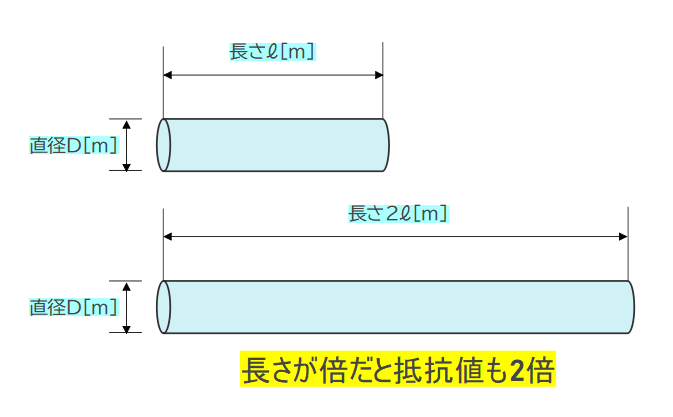
上図のように、直径が同じで、長さが2倍の時
・抵抗値は2倍
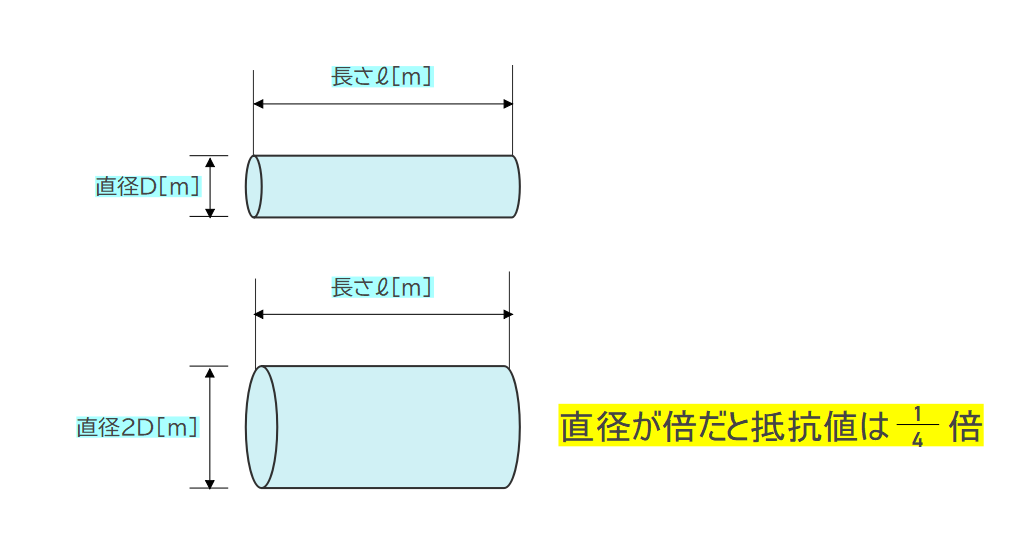
長さが同じで、直径が2倍の時
・抵抗値は\(\displaystyle \frac{1}{4}倍\)
注意点としては、直径が2倍だと、抵抗値が\(\displaystyle \frac{1}{4}倍\)となるので注意してください。
パーセント導電率
パーセント導電率とは、銅(軟銅)の導電率を100%としたときのその他金属等の導体の電流の流れやすさを示したものです。
主な金属のパーセント導電率は以下のようになります。(温度、材料比率等により値は変化します)
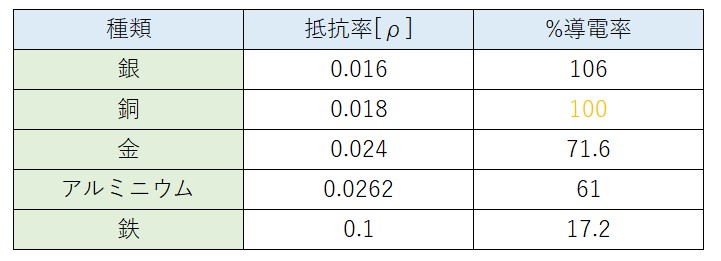
値を覚える必要はありません。
銀がもっとも電気が流れさやすいのですが、価格が高いので電線の材料としては銅がもっとも使用されています。金はもっとも電気が流れやすいとイメージされている方もいるかと思いますが、胴の次の性能となっています、それでも流れやすい方で、加工性が高いためICチップ等の配線に利用されています。
例題1

抵抗の公式より
\(\displaystyle 抵抗R =抵抗率ρ\frac{長さL}{断面積S}[Ω]\)
断面積をまずは求めます。
\(\displaystyle 断面積S= \pi \times (\frac{D}{2})^2=\frac{\pi D^2}{4}\)
こちらを抵抗の公式に当てはめると
\(\displaystyle 抵抗R =ρ\frac{L}{\frac{\pi D^2}{4}}=\frac{4ρL}{\pi D^2}\)
最後に単位を整えると
\(\displaystyle \frac{4ρL}{\pi D^2}\times 10^6\)
となります。
ポイントとしては、最後の答えの式を暗記してもよいかと思います。
あと、この問題に限らないのですが単位を整えるのは最後で大丈夫です。
例題2
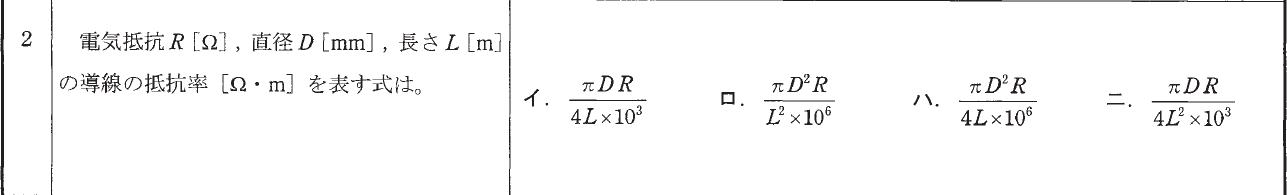
例題1の別バージョンです。
・例題1の式を暗記している場合
\(\displaystyle R=\frac{4ρL}{\pi D^2}\times 10^6\) を展開して
\(\displaystyle ρ=\frac{\pi D^2 R}{4L \times 10^6}\)
・抵抗の公式から求める場合
直径より断面積を求めます(例題1参照)。
\(\displaystyle 抵抗R =ρ\frac{L}{\frac{\pi D^2}{4}}=\frac{4ρL}{\pi D^2}\)
こちらを抵抗率ρ= の式に展開すると
\(\displaystyle ρ=R\frac{\pi D^2}{4L}=\frac{\pi D^2 R}{4L}\)
単位を整えると
\(\displaystyle ρ=\frac{\pi D^2 R}{4L \times 10^6}\)
文系の方は式を見るだけで うわっ となるかもしれませんが、解き方を練習しておけば必ず解けるようになりますので、しっかりできるようにしましょう!

例題3

直径の値より、断面積を求めます。
\(\displaystyle 断面積S= \pi \times (\frac{D}{2})^2=\frac{\pi D^2}{4}=\frac{3.14 \times 2.6^2}{4} \unicode{x2252} 5.3\)[\(mm^2\)]
回答と比較していきます。
・イ 断面積 5.5mm\(^2\), 長さ10m
断面積が近いですので、回答候補
・ロ 断面積 8mm\(^2\), 長さ10m
イと比較すると断面積が広いので違います
・ハ 直径 1.6mm,長さ20m
直径が短く(抵抗が大きくなる)、長さが長い(抵抗が倍になる)のでイと比較して違います
・ニ 直径 3.2mm,長さ5m
直径大きいがやや近い(抵抗が小さくなる),長さが半分(抵抗が半分になる)のでイと比較して違います
ということで、回答は イ となります。
ポイントは、断面積、直径 と2種類の書き方(ちょっとイジワル、)がされているので、断面積を計算して求めましょう!
あとは、回答候補と比較し候補をしぼっていけば解けます。
\(\pi\)の数値は問題の一番最初に \(\pi = 3.14\) と記載があります。電卓が無いので計算めんどいですが、落ち着いて計算しましょう!
全体まとめサイトのご紹介


コメント